概率编程与贝叶斯推断(1)

《贝叶斯方法-概率编程与贝叶斯推断》是本挺不错的书，很适合入门学习。 但书中的示例代码里面有些数据没有提供，自己动手操作可能会麻烦一些。 如果对 python 不熟悉的话，可能安转需要的 Python 库都会遇到一些困难。

先补充一些概率函数相关的知识

贝叶斯的基本思想

与传统的统计推断不同，贝叶斯推断会保留不确定性。古典统计学派认为，概率是事件在长时间内发生的频率。 而贝叶斯派把概率解释为对事件发生的信心。即，概率是观点的概述。某人把概率 0 赋给某个事件的发生，表明他确定此时不会发生。如果除去所有外部信息，那么某人对飞机事故发生的信心， 应该等同于他了解到的飞机事故的频率，和统计派的观点差不多。

每个人都可以对事件赋予概率值，即不存在唯一的概率值。

为了与传统的概率术语对齐，我们把对一个事件 A 发生的信念记为 P(A)，这个值称为先验概率。 用 P(A|X) 表示在得到证据 X 后，A 事件的概率，称为后验概率。

贝叶斯公式

贝叶斯公式(也称为贝叶斯定理)并不等同于贝叶斯推论，在贝叶斯推论中，它仅仅被用来连接先验概率 P(A) 和后验概率 P(A|X)。

概率分布

设 Z 为一个随机变量，那么就存在一个跟 Z 相关的概率分布函数，给定 Z 任何取值， 此函数都得到一个响应的概率值。随机变量可以分 3 种不同类型，离散、连续和混合。

离散情况

如果 Z 是离散的，那么它的分布为概率质量函数。他的度量是当 Z 取值为 k 时的概率， 用 P(Z=k) 标识。概率质量函数完全描述了随机变量 Z，即如果知道 Z 的概率方程， Z 会如何表现都是可知的。

Poisson 分布(帕松分布)

帕松分布是一种常见的分布，其概率质量方程为

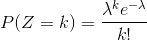
其中 λ 是这个分布的一个参数，决定了此分布的形式。对于帕松分布来说，λ 可以为任意正整数。 k 可以为任意非负整数，如果一个随机变量 Z 存在一个帕松质量分布，可以表示为

Z~Poi(λ)

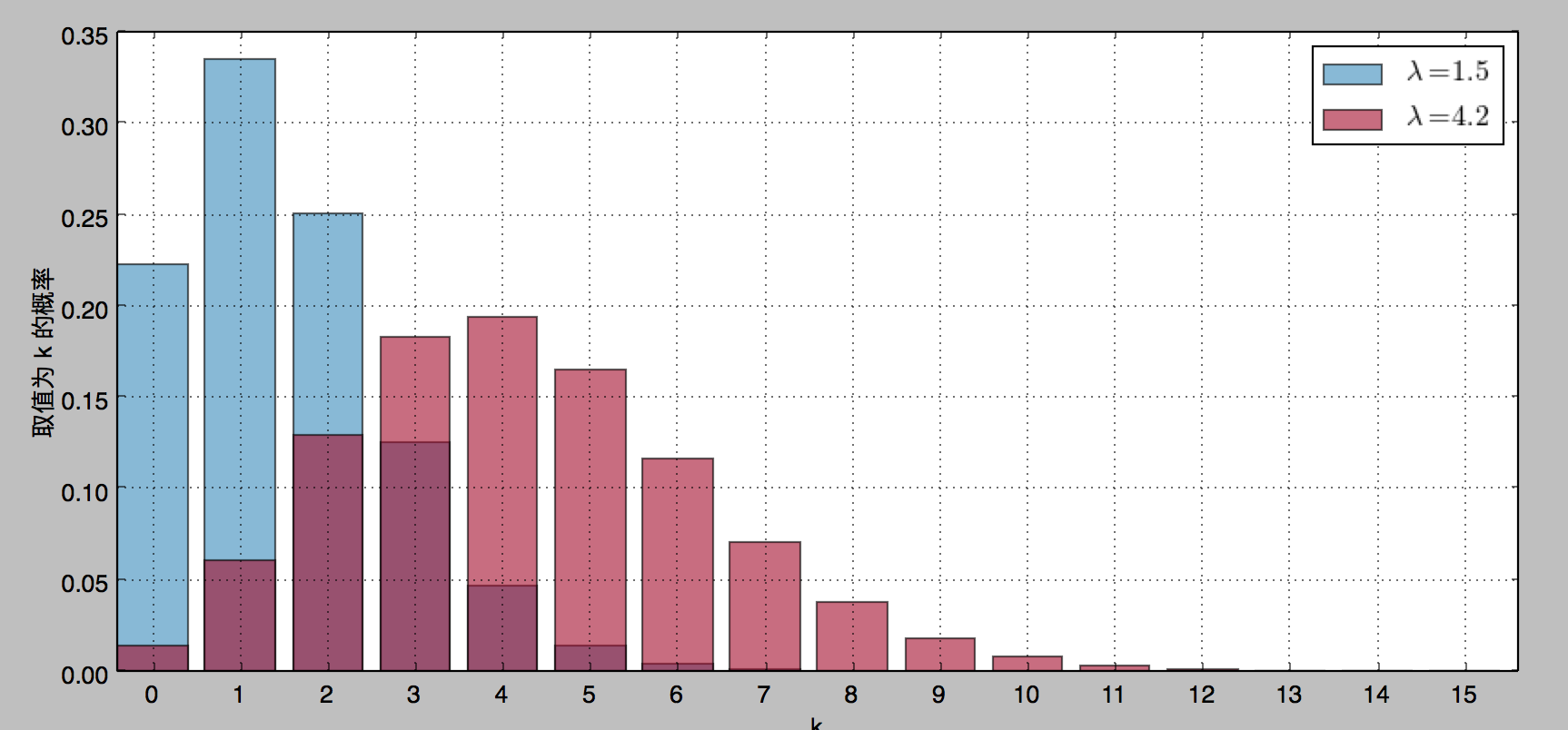
帕松分布的一个重要性质是，它的期望值等于 λ 的取值，即 E[Z|λ] = λ。 下图为帕松分布的两个示例。

连续情况

连续情况下，概率分布函数被称为概率密度函数。概率质量函数和概率密度函数有着本质的不同。

质数密度

指数随机变量的密度函数为

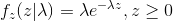
其中 z 的取值可以是任意非负值，当随机变量拥有参数为 λ 的指数分布时，称 Z 服从于指数分布，记为

Z~Exp(λ)

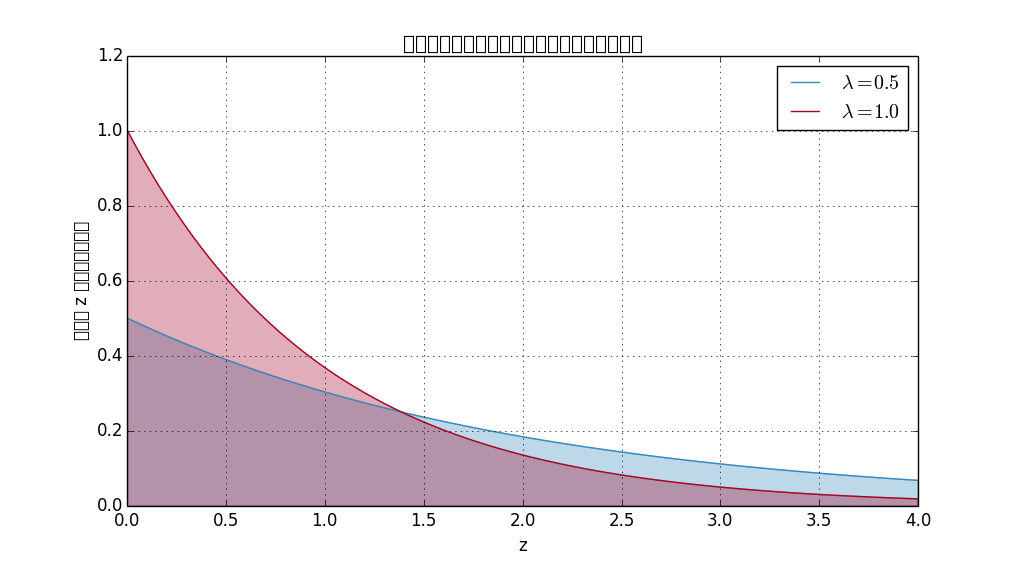
概率密度方程在某一点的值并不等于在这点上的概率。概率密度其实是累积分布函数的微分。 求随机变量落在某个范围内的概率，可以以范围为上下界，对概率密度进行积分。