CSS transform 的基本原理(1)
transform 是什么
CSS 中的 transform 属性，主要用于对元素添加一个变形。可以理解为浏览器完成元素的基本渲染之后， 最后加的一层，并不会对文本流产生任何的影响，其实与 position: relative 的效果一样， 不过不用占用 position 这么重要的一个属性，可以做的变换也不只是平移。
先说 2D 的变换，不涉及 3D。transform 能做的变换有这几种 demo， 分别是缩放、斜切、旋转、平移，以及他们的组合，其中前三个是线性变换。但如果查一下手册， 就会发现，2D 变换中还有一个叫 matrix 的带六个参数的变换。其实平时很少会直接用到 matrix 变换，但对于理解 transform 属性至关重要
matrix 的六个参数是对应一个 3*3 矩阵中的六个变量
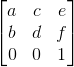
这个矩阵就是 transform 变换的线性变换矩阵。而 transform 中其他的属性，可以说都是 matrix 的语法糖。
线性变换与变换矩阵
这里须要补充一点线性代数的知识了。
首先，什么叫线性变换呢。变换，表示的是一种映射关系，而线性变换，指的是原空间映射到目标空间之后， 依然保持线性关系的变换。
平时我们在 CSS 中定位，使用的是平面直角坐标系，通常用一对数值来表示二维空间中的一个点， 比如 (1, -3) 或者 (0, 0) 之类的，一个是 x 坐标，一个是 y 坐标。
在线性代数里面，坐标可以理解为基向量（也就是在 x 轴上面的单位向量和 y 轴上面的单位向量）的缩放倍数。
也就是说点 (1, 4) 可以理解为一个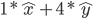 
这样的向量。
因为线性变换前后，线性关系保持不变，也就是说，进行了变换之后，
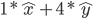这个式子依旧表示同一个点，
只不过他的位置相对于变换前的坐标系，产生了变化。也就是说，只要给出了线性变换后，
基向量相对于原坐标系的值，就能完整地定义这个变换了。
比如说我们进行一个 rotate(90deg) 的变换，那么原坐标系中的基向量 (1, 0)，(0, 1) 会以原点为中心， 顺时针旋转 90°。变成 (0, -1), (1, 0)。假设有一个点 a，在变换前坐标为 (1, 4)， 那变换后的坐标根据上面的公式，可以这样计算出他变换后在原坐标系下的坐标。
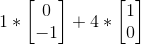
那么就得到线性变换后相对于原坐标系的坐标 (4, -1)，非常完美的一个 90 度旋转。我们把转换后的基向量坐标拼起来， 变成一个 2 * 2 矩阵，就会发现，其实这个计算过程就是矩阵向量乘法。如下图所示
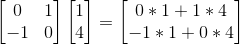
接下来推广这个例子，对于一个线性变换来说，可以找到一对基向量，用等价的基变换来描述。 假设基向量变为 (a, b) 和 (c, d)，那空间中坐标为 (x, y) 的向量经过变换之后， 坐标值可以通过这样求出:
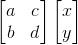
而这个 2 * 2 矩阵，就是我们前面提到的线性变换矩阵了。
平移
但还是有一个问题，CSS transform 中的 matrix 属性，变换矩阵是一个 3 * 3 矩阵，刚刚我们推导出来的， 是一个 2 * 2 矩阵啊，到底是哪里出了问题？其实关键就在于 transform 支持了平移操作 translate。 平移并不是一个线性变换操作，因为平移改变了原点，使得变换前后的线性关系不成立了。
为了将平移操作纳入变换矩阵中，须要给矩阵额外增加一个维度。回到一开始说到的那个矩阵。
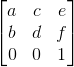
如果 2 * 2 的矩阵代表的是两个 2 维基向量，那么 3 * 3 矩阵意味着，这其实是一个 3 维变换， 即这个矩阵可以按列分解为 3 个 3 维向量，分别代表变换后的 3 个基向量。
相应的，在计算时，我们的二维向量 (x, y) 也会被补齐为 (x, y, 1)。思考一下，这样添加的第三列中的 e, f 与平移究竟是什么关系。
考虑这样一个 matrix 属性
div {
transform: matrix(1, 0, 0, 1, 2, 0);
}按照之前的介绍，前四个参数，表示 x 轴单位向量和 y 轴单位向量，在变换前后没有变化。 而后两个参数，与补齐的最后一位组成了一个 3 维向量 (2, 0, 1)，也就是说 z 轴的单位向量， 在变换后，变成了 (2, 0, 1)。看下图可能感受会直观一些（注意坐标轴的标识）：
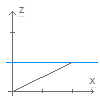
其中蓝色的直线，代表了我们的二维平面，只不过在侧面观察，就只能是一条线了。如果不考虑 Z 轴的话，相当于平面的原点向右移动了两个单位。对，没有错，这其实就是 3 维上面的 skew，斜切操作。 用高维度的斜切操作来代替低纬度的平移，就可以很巧妙地把平移这个非线性的操作归入到线性变换矩阵中了。
但是，又有什么用呢
这些东西实际上确实不会用到，但不要着急，请期待下一期。